In this tutorial, we’ll be building a transformer-based model for Handwritten Mathematical Expression Recognition (HMER). While the output of the model is LaTeX text, the input is a set of images rendered from stroke data making this an offline task. The online variation of this task would see us directly using the stroke data, which in addition to coordinates, can include useful attributes like pen pressure and timestamp data.
Although this task dates back to the 1960s, the first Competition on Recognition of Online Handwritten Mathematical Expressions (CROHME) was held at the International Conference on Document Analysis and Recognition (ICDAR) in 2011. Since then it has been run many times, most recently in 2023. We’ll be using the CROHME 2023 dataset1 to train this model.
Tokenization
Tokenization is an important first step in making the LaTeX text interpretable by a Machine Learning model. Instead of using Hugging Face Tokenizers2, a powerful library that includes tokenization algorithms such as Byte-Pair Encoding (BPE) and WordPiece, we’ll build our own basic tokeniser, LaTeXTokenizer, from scratch so that we can peer into how tokenization, vocabulary building, and encoding/decoding work.
import collections
import re
from typing import Dict, List, Tuple, Union
class LaTeXTokenizer:
def __init__(self):
self.special_tokens = ["[PAD]", "[BOS]", "[EOS]", "[UNK]"]
self.vocab = {}
self.token_to_id = {}
self.id_to_token = {}
def tokenize(self, text: str) -> List[str]:
# Tokenize LaTeX using regex to capture commands, numbers and other characters
return re.findall(r"\\[a-zA-Z]+|\\.|[a-zA-Z0-9]|\S", text)
def build_vocab(self, texts: List[str]):
# Add special tokens to vocabulary
for token in self.special_tokens:
self.vocab[token] = len(self.vocab)
# Create a counter to hold token frequencies
counter = collections.Counter()
# Tokenize each text and update the counter
for text in texts:
tokens = self.tokenize(text)
counter.update(tokens)
# Add tokens to vocab based on their frequency
for token, _ in counter.most_common():
if token not in self.vocab:
self.vocab[token] = len(self.vocab)
# Build dictionaries for token to ID and ID to token conversion
self.token_to_id = self.vocab
self.id_to_token = {v: k for k, v in self.vocab.items()}
def encode(self, text: str) -> List[int]:
# Tokenize the input text and add start and end tokens
tokens = ["[BOS]"] + self.tokenize(text) + ["[EOS]"]
# Map tokens to their IDs, using [UNK] for unknown tokens
unk_id = self.token_to_id["[UNK]"]
return [self.token_to_id.get(token, unk_id) for token in tokens]
def decode(self, token_ids: List[int]) -> List[str]:
# Map token IDs back to tokens
tokens = [self.id_to_token.get(id, "[UNK]") for id in token_ids]
# Remove tokens beyond the [EOS] token
if "[EOS]" in tokens:
tokens = tokens[: tokens.index("[EOS]")]
# Replace [UNK] with ?
tokens = ["?" if token == "[UNK]" else token for token in tokens]
# Reconstruct the original text, ignoring special tokens
return "".join([token for token in tokens if token not in self.special_tokens])
I’d like to highlight several interesting aspects of the LaTeXTokenizer code:
- we designate 4 special tokens that aid us in various downstream tasks: a padding token
[PAD], a beginning of sentence token[BOS], an end of sentence token[EOS]and an unknown token[UNK] - we use the regular expression
\\[a-zA-Z]+|\\.|[a-zA-Z0-9]|\Sto capture LaTeX commands, numbers, and other characters - decoded LaTeX strings are truncated upon encountering an
[EOS]token - encoded tokens are prefixed by the
[BOS]token and suffixed with the[EOS]token - encoded tokens that are not in the vocabulary are designed
[UNK], meaning that they weren’t seen during training and are only seen during val/test/predict time
Let’s have a look at the LaTeXTokenizer class in action.
Vocabulary Building
First, let’s instantiate the LaTeXTokenizer class and build the vocabulary with two example mathematical expressions written in LaTeX: a^2 + b^2 = c^2 and e^{i\pi} + 1 = 0.
tokenizer = LaTeXTokenizer()
tokenizer.build_vocab(["a^2 + b^2 = c^2", "e^{i\\pi} + 1 = 0"])
After running this code snippet, you can inspect the vocabulary to see the tokens and their corresponding IDs.
print(tokenizer.vocab)
{'[PAD]': 0, '[BOS]': 1, '[EOS]': 2, '[UNK]': 3, '^': 4, '2': 5, '+': 6, '=': 7, 'a': 8, 'b': 9, 'c': 10, 'e': 11, '{': 12, 'i': 13, '\\pi': 14, '}': 15, '1': 16, '0': 17}
Notice that the special tokens [PAD], [BOS], [EOS] and [UNK] are also present in the vocabulary.
Encoding
Now let’s encode a new mathematical expression, $i^2 = -1$, into its corresponding token IDs. The encode method will tokenize the input string and convert each token into its respective ID from the vocabulary. Unknown tokens, if any, will be mapped to [UNK].
ids = tokenizer.encode('i^2 = -1')
print(ids)
[1, 13, 4, 5, 7, 3, 16, 2]
Decoding
Finally, to check that the encoding makes sense, we decode the token IDs back into a LaTeX string. The decode method will convert the token IDs back to their original LaTeX tokens, joining them into a LaTeX expression.
latex = tokenizer.decode(ids)
print(latex)
i^2=?1
Notice that the minus symbol (-) was not present in the vocabulary and so was encoded into [UNK], represented in the decoded string as a ?.
CROHME Dataset
The CROHME dataset is a collection of handwritten mathematical expressions with their corresponding LaTeX annotations. In this section, we’ll be parsing the dataset’s InkML files and preparing them for model training.
InkML is a data format for representing digital ink entered with an electronic pen. It supports many attributes including writer information (like age, gender, and handedness), pen pressure, pen tilt, stroke data, and ground truth data. For our purpose, we’ll only be using the stroke data and ground truth LaTeX string, which we parse using the parse_inkml function. Instead of rendering the stroke data and extracting the LaTeX string on-the-fly, as data gets loaded into the model, we cache them to the filesystem to speed things up.
import io
import matplotlib.pyplot as plt
import xml.etree.ElementTree as ET
from pathlib import Path
from PIL import Image
def parse_inkml(inkml_file_path, ns={"inkml": "http://www.w3.org/2003/InkML"}):
tree = ET.parse(inkml_file_path)
root = tree.getroot()
strokes = []
for trace in root.findall(".//inkml:trace", ns):
coords = trace.text.strip().split(",")
coords = [
(float(x), -float(y)) # Invert y-axis to match InkML's coordinate system
for x, y, *z in [coord.split() for coord in coords]
]
strokes.append(coords)
latex = root.find('.//inkml:annotation[@type="truth"]', ns).text.strip(" $")
return strokes, latex
def cache_data():
fig, ax = plt.subplots()
for inkml_file in data_dir.glob("*/*.inkml"):
img_file = inkml_file.with_suffix(".png")
txt_file = inkml_file.with_suffix(".txt")
strokes, latex = parse_inkml(inkml_file)
# Write LaTeX to file
with open(txt_file, "w") as f:
f.write(latex)
# Render strokes to file
ax.set_axis_off()
ax.set_aspect("equal")
for coords in strokes:
x, y = zip(*coords)
ax.plot(x, y, color="black", linewidth=2)
buf = io.BytesIO()
plt.savefig(buf, bbox_inches="tight", pad_inches=0)
plt.cla()
buf.seek(0)
img = Image.open(buf).convert("RGB")
img.save(img_file)
cache_data()
Next, we wrap CROHMEDataset around this cached image and LaTeX data, storing the corresponding train/val splits in a CROHMEDataModule. The collate_fn method takes care of centering and padding images within a fixed size canvas as well as padding token sequences to the maximum length of the batch. The images are randomly distorted using RandomPerspective to make the model more robust.
import lightning.pytorch as pl
import torch
import torch.nn.functional as F
from pathlib import Path
from PIL import Image
from torch import nn, optim, Tensor
from torch.nn.utils.rnn import pad_sequence
from torch.utils import data
from torchvision import transforms
class CROHMEDataset(data.Dataset):
def __init__(self, latex_files, tokenizer, transform):
super().__init__()
self.latex_files = list(latex_files)
self.tokenizer = tokenizer
self.transform = transform
def __len__(self):
return len(self.latex_files)
def __getitem__(self, idx):
latex_file = self.latex_files[idx]
image_file = latex_file.with_suffix(".png")
with open(latex_file) as f:
latex = f.read()
x = self.transform(Image.open(image_file))
y = Tensor(self.tokenizer.encode(latex))
return x, y
class CROHMEDataModule(pl.LightningDataModule):
def __init__(
self,
data_dir: str,
batch_size: int = 1,
num_workers: int = 0,
pin_memory: bool = False,
):
super().__init__()
self.save_hyperparameters()
self.data_dir = Path(data_dir)
self.transform = transforms.Compose(
[
transforms.RandomPerspective(distortion_scale=0.1, p=0.5, fill=255),
transforms.ToTensor(),
]
)
def setup(self, stage):
latexes = []
for latex_file in self.data_dir.glob("train/*.txt"):
with open(latex_file) as f:
latexes.append(f.read())
self.tokenizer = LaTeXTokenizer()
self.tokenizer.build_vocab(latexes)
self.vocab_size = len(self.tokenizer.vocab)
if stage == "fit" or stage is None:
self.train_dataset = CROHMEDataset(
self.data_dir.glob("train/*.txt"), self.tokenizer, self.transform
)
self.val_dataset = CROHMEDataset(
self.data_dir.glob("val/*.txt"), self.tokenizer, self.transform
)
def collate_fn(self, batch, max_width: int = 512, max_height: int = 384):
images, labels = zip(*batch)
# Create a white background for each image in the batch
src = torch.ones((len(images), 3, max_height, max_width))
# Center and pad individual images to fit into the white background
for i, img in enumerate(images):
height_start = (max_height - img.size(1)) // 2
height_end = height_start + img.size(1)
width_start = (max_width - img.size(2)) // 2
width_end = width_start + img.size(2)
src[i, :, height_start:height_end, width_start:width_end] = img
# Pad sequences for labels and create attention mask
tgt = pad_sequence(labels, batch_first=True).long()
seq_len = tgt.size(1)
tgt_mask = torch.triu(torch.ones(seq_len, seq_len) * float("-inf"), diagonal=1)
return src, tgt, tgt_mask
def train_dataloader(self):
return data.DataLoader(
self.train_dataset,
batch_size=self.hparams.batch_size,
num_workers=self.hparams.num_workers,
collate_fn=self.collate_fn,
pin_memory=self.hparams.pin_memory,
)
def val_dataloader(self):
return data.DataLoader(
self.val_dataset,
batch_size=self.hparams.batch_size,
num_workers=self.hparams.num_workers,
collate_fn=self.collate_fn,
pin_memory=self.hparams.pin_memory,
)
Visualising a Batch of Data
Let’s inspect a batch of data to see what’s being fed to the model.
datamodule = CROHMEDataModule("../data/CROHME/", batch_size=16)
datamodule.setup(stage="fit")
tokenizer = datamodule.tokenizer
train_dataloader = datamodule.train_dataloader()
batch = next(iter(train_dataloader))
src, tgt, tgt_mask = batch
Here,
srccontains the images of the handwritten mathematical expressions;tgtcontains the token IDs representing the LaTeX expressions; andtgt_maskis the attention mask, which we’ll explain later on.
Handwritten Image
from torchvision.utils import make_grid
plt.imshow(make_grid(src, nrow=4).permute(1, 2, 0))
plt.axis("off")
(-0.5, 2057.5, 1545.5, -0.5)
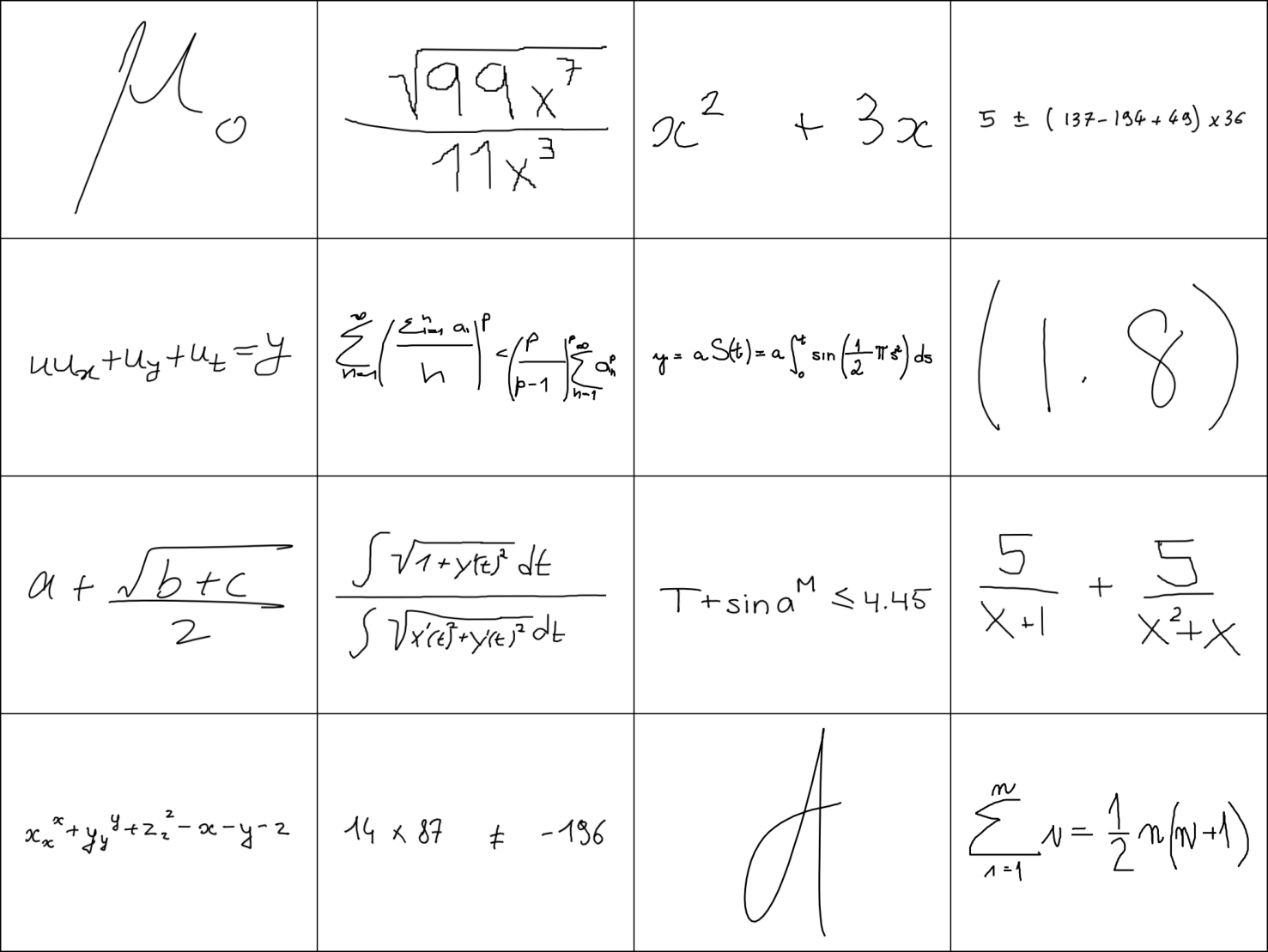
LaTeX String
for t in tgt:
print(tokenizer.decode(t.tolist()))
{\mu}{o} \frac{\sqrt{99{x^{7}}}}{11{x^{3}}} x^2+3x 5\pm(137-194+49)\times36 uu{x}+u{y}+u{t}=y \sum{n=1}^{\infty}{(\frac{\sum{i=1}^{n}a{i}}{n})^{p}}\lt{(\frac{p}{p-1})^{p}}\sum{n=1}^{\infty}{a{n}^{p}} y=aS(t)=a\int_0^{t}\sin(\frac{1}{2}\pis^2)ds \left(1.8\right) a+\frac{\sqrt{b+c}}{2} \frac{\int\sqrt{1+{y^{‘}(t)^{2}}}dt}{\int\sqrt{{x^{‘}(t)^{2}}+{y^{‘}(t)^{2}}}dt} {{T+\sin{a}^{M}}\leq4.45} \frac{5}{x+1}+\frac{5}{{x^{2}}+x} x_x^x+y_y^y+z_z^z-x-y-z 14\times87\neq-196 \mbox{d} \sum{i=1}^{n}i=\frac{1}{2}n(n+1)
Positional Encoding for Attention Models
In models like Transformers, positional information is not naturally captured by the self-attention mechanism. For this reason, we use a technique called positional encoding to give the model information about the relative positions of the tokens. Ensuring that the model can take into account the order of the tokens allows it to significantly improve its performance on sequence-based tasks.
We’ll be using two types of positional encodings: 1D and 2D positional encodings, which are essential for 1D sequences like text and 2D structures like images, respectively.
-
In the 1D case, each position in the sequence is encoded into a high-dimensional vector. We use sine and cosine functions of different frequencies to encode the positional information.
-
When dealing with images or any 2D data, a 2D positional encoding is more appropriate. Here, we use a similar technique but extend it to 2D. We calculate 1D positional encoding first and then use the outer product to construct the 2D positional encoding. This way, each position in a 2D structure (like an image) gets a unique encoding based on its row and column.
import math
import matplotlib.pyplot as plt
class PositionalEncoding1D(nn.Module):
def __init__(
self,
d_model: int,
dropout: float = 0.1,
max_len: int = 1000,
temperature: float = 10000.0,
):
super().__init__()
# Generate position and dimension tensors for encoding
position = torch.arange(max_len).unsqueeze(1)
dim_t = torch.arange(0, d_model, 2)
div_term = torch.exp(dim_t * (-math.log(temperature) / d_model))
# Initialize and fill the positional encoding matrix with sine/cosine values
pe = torch.zeros(max_len, d_model)
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
self.dropout = nn.Dropout(dropout)
self.register_buffer("pe", pe)
def forward(self, x):
batch, sequence_length, d_model = x.shape
return self.dropout(x + self.pe[None, :sequence_length, :])
class PositionalEncoding2D(nn.Module):
def __init__(
self,
d_model: int,
dropout: float = 0.1,
max_len: int = 30,
temperature: float = 10000.0,
):
super().__init__()
# Generate position and dimension tensors for 1D encoding
position = torch.arange(max_len).unsqueeze(1)
dim_t = torch.arange(0, d_model, 2)
div_term = torch.exp(dim_t * (-math.log(temperature) / d_model))
# Initialize and fill the 1D positional encoding matrix with sine/cosine values
pe_1D = torch.zeros(max_len, d_model)
pe_1D[:, 0::2] = torch.sin(position * div_term)
pe_1D[:, 1::2] = torch.cos(position * div_term)
# Compute the 2D positional encoding matrix using outer product
pe_2D = torch.zeros(max_len, max_len, d_model)
for i in range(d_model):
pe_2D[:, :, i] = pe_1D[:, i].unsqueeze(-1) + pe_1D[:, i].unsqueeze(0)
self.dropout = nn.Dropout(dropout)
self.register_buffer("pe", pe_2D)
def forward(self, x):
batch, height, width, d_model = x.shape
return self.dropout(x + self.pe[None, :height, :width, :])
Visualising Positional Encodings with Python
Understanding positional encodings can become much clearer when you visualise them.
1D Positional Encoding

First, we will create a 1D positional encoding with a d_model of 256 and a maximum length of 100. We will then use matshow from Matplotlib to display it as a heatmap that reflects the values of the positional encoding. The x-axis represents the dimension (d_model) and the y-axis represents the sequence length (up to max_len).
2D Positional Encoding
For the 2D positional encoding, we use a more complex visualisation. We create a 2D positional encoding with d_model set to 32 and max_len to 64. Each subplot below show different layers (or dimensions) of the 2D positional encoding, allowing you to see how each dimension encodes 2D positional information differently.

Transformer-based Model
While a range of architectures are suitable for sequence-based tasks, the Transformer-approach is particularly versatile. In our case, the image is encoded into a set of features, which is then decoded autoregressively.
-
Encoder: The encoder is based on the DenseNet121 architecture. Since DenseNet was trained to output the 1,000 ImageNet classes, we swap the final classifier layer with a 1×1 convolution to reduce the output to
d_modeldimensions. We add the 2D positional encodings before flattening it into a sequence to be consumed by the decoder. -
Decoder: The decoder is a stack of transformer layers that takes both the source features from the encoder and the target text. The target text is embedded into
d_model-dimensional vectors and augmented with 1D positional encodings. After that, the source features and target embeddings are processed through the transformer decoder stack to generate the output. The last fully connected layer (fc_out) maps the output of the transformer to the vocabulary size, effectively determining the next token’s likelihood in the sequence.
Training
During training, the encoder’s output features and a shifted copy of the target sequence are fed into the decoder. The model’s predictions are then compared to the actual target sequence to compute the loss, which is then backpropagated to update the model parameters.
As mentioned above, the attention mask is one of the inputs to the model, along with the handwritten image and the LaTeX. In autoregressive decoding, its purpose is to ensure that each token is predicted based only on previously generated tokens as well as the encoded representation. In the example attention mask below, cells shaded white are what we are allowed to see, while cells shaded grey are hidden. To predict the 0-th target token {, we are only allowed to see the [BOS] token. Jumping to the 6-th row, to predict the 6-th target token }, we are only allowed to see the token sequence [BOS], {, \mu, }, _, {, o.

Inference
During inference, we can use either greedy search or beam search to generate sequences. In both methods, the initial step starts with feeding the encoder’s output features into the decoder, followed by iterative steps to generate each subsequent token.
-
Greedy Search: In greedy decoding, the model chooses the most likely (highest probability) next step at each step in the sequence. This is computationally less expensive but may not always produce the most optimal sequences. During inference, we start with a
[BOS]token and keep appending the token with the highest probability to the target sequence until it reachesmax_seq_lenor a[EOS]token is encountered. -
Beam Search: Beam search keeps track of the top
k(beam width) probable sequences at each step, expanding all of them at each step and keeping only the bestk. This is computationally more expensive but usually produces better results. During inference, we start with a[BOS]token and and maintain multiple sequences for each item in the batch, updating them at each step based on their total log probability so far. Again, candidate sequences are stopped when[EOS]tokens are encountered and their scores frozen.
from torchvision.models import densenet121, DenseNet121_Weights
class Permute(nn.Module):
def __init__(self, *dims: int):
super().__init__()
self.dims = dims
def forward(self, x):
return x.permute(*self.dims)
class Model(pl.LightningModule):
def __init__(
self,
vocab_size: int,
d_model: int,
nhead: int,
dim_feedforward: int,
dropout: float,
num_layers: int,
lr: float = 1e-4,
):
super().__init__()
self.save_hyperparameters()
self.example_input_array = (
torch.rand(16, 3, 384, 512), # batch x channel x height x width
torch.ones(16, 64, dtype=torch.long), # batch x sequence length
torch.zeros(64, 64), # sequence length x sequence length
)
# Define the encoder architecture
densenet = densenet121(weights=DenseNet121_Weights.DEFAULT)
self.encoder = nn.Sequential(
nn.Sequential(*list(densenet.children())[:-1]), # remove the final layer
nn.Conv2d(1024, d_model, kernel_size=1),
Permute(0, 2, 3, 1),
PositionalEncoding2D(d_model, dropout),
nn.Flatten(1, 2),
)
# Define the decoder architecture
self.tgt_embedding = nn.Embedding(vocab_size, d_model, padding_idx=0)
self.word_positional_encoding = PositionalEncoding1D(d_model, dropout)
self.transformer_decoder = nn.TransformerDecoder(
nn.TransformerDecoderLayer(
d_model, nhead, dim_feedforward, dropout, batch_first=True
),
num_layers,
)
self.fc_out = nn.Linear(d_model, vocab_size)
def decoder(self, features, tgt, tgt_mask):
padding_mask = tgt.eq(0)
tgt = self.tgt_embedding(tgt) * math.sqrt(self.hparams.d_model)
tgt = self.word_positional_encoding(tgt)
tgt = self.transformer_decoder(
tgt, features, tgt_mask=tgt_mask, tgt_key_padding_mask=padding_mask
)
output = self.fc_out(tgt)
return output
def forward(self, src, tgt, tgt_mask):
features = self.encoder(src)
output = self.decoder(features, tgt, tgt_mask)
return output
def training_step(self, batch, batch_idx):
loss = self._shared_eval_step(batch, batch_idx)
self.log(
"train_loss",
loss,
on_step=True,
on_epoch=True,
sync_dist=True,
prog_bar=True,
)
return loss
def validation_step(self, batch, batch_idx):
loss = self._shared_eval_step(batch, batch_idx)
metrics = {"val_loss": loss}
self.log_dict(metrics, sync_dist=True)
return metrics
def _shared_eval_step(self, batch, batch_idx):
src, tgt, tgt_mask = batch
tgt_in = tgt[:, :-1]
tgt_out = tgt[:, 1:]
output = self(src, tgt_in, tgt_mask[:-1, :-1])
loss = F.cross_entropy(
output.reshape(-1, self.hparams.vocab_size),
tgt_out.reshape(-1),
ignore_index=0,
)
return loss
def beam_search(
self,
src,
tokenizer,
max_seq_len: int = 256,
beam_width: int = 3,
) -> List[str]:
with torch.no_grad():
batch_size = src.size(0)
vocab_size = self.hparams.vocab_size
features = self.encoder(src).detach()
features_rep = features.repeat_interleave(beam_width, dim=0)
tgt_mask = torch.triu(
torch.ones(max_seq_len, max_seq_len) * float("-inf"), diagonal=1
).to(src.device)
# Initialize with [BOS]
beams = torch.ones(batch_size, 1, 1).long().to(src.device)
# Handle first step separately
output = self.decoder(features, beams[:, 0, :], tgt_mask[:1, :1])
next_probs = output[:, -1, :].log_softmax(dim=-1)
beam_scores, indices = next_probs.topk(beam_width, dim=-1)
beams = torch.cat(
[beams.repeat_interleave(beam_width, dim=1), indices.unsqueeze(2)],
dim=-1,
)
for i in range(2, max_seq_len):
tgt = beams.view(batch_size * beam_width, i)
output = self.decoder(features_rep, tgt, tgt_mask[:i, :i])
next_probs = output[:, -1, :].log_softmax(dim=-1)
next_probs += beam_scores.view(batch_size * beam_width, 1)
next_probs = next_probs.view(batch_size, -1)
beam_scores, indices = next_probs.topk(beam_width, dim=-1)
beams = torch.cat(
[
beams[
torch.arange(batch_size).unsqueeze(-1),
indices // vocab_size,
],
(indices % vocab_size).unsqueeze(2),
],
dim=-1,
)
best_beams = beams[:, 0, :] # taking the best beam for each batch
return [tokenizer.decode(seq.tolist()) for seq in best_beams]
def greedy_search(self, src, tokenizer, max_seq_len: int = 256) -> List[str]:
with torch.no_grad():
batch_size = src.size(0)
features = self.encoder(src).detach()
tgt = torch.ones(batch_size, 1).long().to(src.device)
tgt_mask = torch.triu(
torch.ones(max_seq_len, max_seq_len) * float("-inf"), diagonal=1
).to(src.device)
for i in range(1, max_seq_len):
output = self.decoder(features, tgt, tgt_mask[:i, :i])
next_probs = output[:, -1].log_softmax(dim=-1)
next_chars = next_probs.argmax(dim=-1, keepdim=True)
tgt = torch.cat((tgt, next_chars), dim=1)
return [tokenizer.decode(seq.tolist()) for seq in tgt]
def configure_optimizers(self):
optimizer = optim.Adam(self.parameters(), lr=self.hparams.lr)
scheduler = optim.lr_scheduler.ReduceLROnPlateau(
optimizer, patience=3, verbose=True
)
return {
"optimizer": optimizer,
"lr_scheduler": {"scheduler": scheduler, "monitor": "val_loss"},
}
import wandb
from lightning.pytorch.callbacks import Callback
class LogPredictionSamples(Callback):
def on_validation_batch_end(
self, trainer, pl_module, outputs, batch, batch_idx, dataloader_idx=0
):
if batch_idx == 0: # log samples only for the first batch of validation data
src, tgt, tgt_mask = batch
tokenizer = trainer.datamodule.tokenizer
epoch = pl_module.current_epoch
images = [wandb.Image(img) for img in src]
targets = [tokenizer.decode(seq.tolist()) for seq in tgt]
beams = pl_module.beam_search(src, tokenizer)
greedys = pl_module.greedy_search(src, tokenizer)
wandb_logger.log_text(
key="sample_latex",
columns=["epoch", "image", "target", "beam", "greedy"],
data=[
[epoch, i, t, b, g]
for i, t, b, g in zip(images, targets, beams, greedys)
],
)
Training the Model
We train the model using PyTorch Lightning, making use of 3 callbacks:
-
EarlyStopping: Stops the training process if the validation loss doesn’t improve for six consecutive epochs, which helps avoid overfitting.
-
ModelSummary: Provides a summary of the model architecture, which can be useful for debugging or profiling.
-
LogPredictionSamples: Although not explicitly defined here, I presume this custom callback logs samples of the model’s predictions during training for further analysis.
Using 2 × NVIDIA Quadro GP100, and the hyperparameters found in this paper3, the model takes 1 hour to train.
from lightning.pytorch.callbacks.model_summary import ModelSummary
from lightning.pytorch.callbacks.early_stopping import EarlyStopping
wandb_logger = pl.loggers.WandbLogger()
datamodule = CROHMEDataModule(
"../data/CROHME/", batch_size=16, num_workers=8, pin_memory=True
)
datamodule.setup(stage="fit")
model = Model(datamodule.vocab_size, 256, 8, 1024, 0.2, 3)
early_stopping = EarlyStopping(monitor="val_loss", patience=6, verbose=True)
model_summary = ModelSummary(max_depth=2)
log_prediction_samples = LogPredictionSamples()
trainer = pl.Trainer(
max_epochs=-1,
logger=wandb_logger,
callbacks=[early_stopping, model_summary, log_prediction_samples],
accelerator="gpu",
devices=2,
)
trainer.fit(model=model, datamodule=datamodule)
Reviewing the Outputs
By setting the model to eval mode, dropout is turned off in order to produce the best prediction possible. Below, we use a single batch to compare the outputs of the model using greedy decoding and beam search, with the ground truth.
model.eval()
beam_preds = model.beam_search(src.to(model.device), tokenizer, max_seq_len=256)
greedy_preds = model.greedy_search(src.to(model.device), tokenizer, max_seq_len=256)
tgt_preds = [tokenizer.decode(t.tolist()) for t in tgt]
import pandas as pd
df = pd.DataFrame(
{
"ground_truth": tgt_preds,
"beam_search": beam_preds,
"greedy_decoding": greedy_preds,
}
)
df
| ground_truth | beam_search | greedy_decoding | |
|---|---|---|---|
| 0 | {\mu}_{o} | {\mu}_{\mbox{o}} | {\mu}_{o} |
| 1 | \frac{\sqrt{99{x^{7}}}}{11{x^{3}}} | \frac{\sqrt{99{x^{7}}}}{11{x^{3}}}} | \frac{\sqrt{99{x^{7}}}}{11{x^{3}}} |
| 2 | x^2+3x | x^2+3x | x^2+3x |
| 3 | 5\pm(137-194+49)\times36 | 5\pm(137-194+49)\times36 | 5\pm(137-194+49)\times36 |
| 4 | uu_{x}+u_{y}+u_{t}=y | uu_{x}+u_{y}+u_{t}=y | uu_{x}+u_{y}+u_{t}=y |
| 5 | \sum_{n=1}^{\infty}{(\frac{\sum_{i=1}^{n}a_{i}}{n})^{p}}\lt{(\frac{p}{p-1})^{p}}\sum_{n=1}^{\infty}{a_{n}^{p}} | \sum_{n=1}^{\infty}{(\frac{\sum_{i=1}^{n}a_{n}}{n})^{p}}\lt{(\frac{p}{p-1})^{p}{p}\sum_{n=1}^{\infty}{\infty}^{p} | \sum_{n=1}^{\infty}{(\frac{\sum_{i=1}^{n}a_{i}}{n})^{p}}\lt{(\frac{p}{p})^{p}{p}\sum_{n=1}^{p}^{p}}{p} |
| 6 | y=aS(t)=a\int_0^{t}\sin(\frac{1}{2}\pis^2)ds | y=aS(t)=a\int_0^{t}\sin(\frac{1}{2}\pis^2)ds | y=aS(t)=a\int_0^{t}\sin(\frac{1}{2}\pis^2)ds |
| 7 | \left(1.8\right) | \left(1.8\right) | \left(1.8\right) |
| 8 | a+\frac{\sqrt{b+c}}{2} | a+\frac{\sqrt{b+c}}{2} | a+\frac{\sqrt{b+c}}{2} |
| 9 | \frac{\int\sqrt{1+{y^{‘}(t)^{2}}}dt}{\int\sqrt{{x^{‘}(t)^{2}}+{y^{‘}(t)^{2}}}dt} | \frac{\int\sqrt{1+{y^{2}(t)^{2}}dt}dt}{\int\sqrt{{x^{2}}+{y^{2}}}} | \frac{\int\sqrt{1+{y^{2}(t)^{2}}dt}dt}{\int\sqrt{x^{2}}} |
| 10 | {{T+\sin{a}^{M}}\leq4.45} | {T+\sin{a^{M}}\leq4.45} | {T+\sin{a^{M}}\leq4.45} |
| 11 | \frac{5}{x+1}+\frac{5}{{x^{2}}+x} | \frac{5}{x+1}+\frac{5}{{x^{2}}+x} | \frac{5}{x+1}+\frac{5}{{x^{2}}+x} |
| 12 | x_x^x+y_y^y+z_z^z-x-y-z | x_x^x+y_y^y+z_z^z-x-y-z | x_x^x+y_y^y+z_z^z-x-y-z |
| 13 | 14\times87\neq-196 | 14\times87\neq-196 | 14\times87\neq-196 |
| 14 | \mbox{d} | \mbox{d} | \mbox{d} |
| 15 | \sum_{i=1}^{n}i=\frac{1}{2}n(n+1) | \sum_{i=1}^{n}i=\frac{1}{2}n(n+1) | \sum_{i=1}^{n}i=\frac{1}{2}n(n+1) |
And in rendered LaTeX:
for c in df.columns:
df[c] = "$$" + df[c].astype(str) + "$$"
df
| ground_truth | beam_search | greedy_decoding | |
|---|---|---|---|
| 0 | \({\mu}_{o}\) | \({\mu}_{\mbox{o}}\) | \({\mu}_{o}\) |
| 1 | \(\frac{\sqrt{99{x^{7}}}}{11{x^{3}}}\) | \(\frac{\sqrt{99{x^{7}}}}{11{x^{3}}}}\) | \(\frac{\sqrt{99{x^{7}}}}{11{x^{3}}}\) |
| 2 | \(x^2+3x\) | \(x^2+3x\) | \(x^2+3x\) |
| 3 | \(5\pm(137-194+49)\times36\) | \(5\pm(137-194+49)\times36\) | \(5\pm(137-194+49)\times36\) |
| 4 | \(uu_{x}+u_{y}+u_{t}=y\) | \(uu_{x}+u_{y}+u_{t}=y\) | \(uu_{x}+u_{y}+u_{t}=y\) |
| 5 | \(\sum_{n=1}^{\infty}{(\frac{\sum_{i=1}^{n}a_{i}}{n})^{p}}\lt{(\frac{p}{p-1})^{p}}\sum_{n=1}^{\infty}{a_{n}^{p}}\) | \(\sum_{n=1}^{\infty}{(\frac{\sum_{i=1}^{n}a_{n}}{n})^{p}}\lt{(\frac{p}{p-1})^{p}{p}\sum_{n=1}^{\infty}{\infty}^{p}\) | \(\sum_{n=1}^{\infty}{(\frac{\sum_{i=1}^{n}a_{i}}{n})^{p}}\lt{(\frac{p}{p})^{p}{p}\sum_{n=1}^{p}^{p}}{p}\) |
| 6 | \(y=aS(t)=a\int_0^{t}\sin(\frac{1}{2}\pis^2)ds\) | \(y=aS(t)=a\int_0^{t}\sin(\frac{1}{2}\pis^2)ds\) | \(y=aS(t)=a\int_0^{t}\sin(\frac{1}{2}\pis^2)ds\) |
| 7 | \(\left(1.8\right)\) | \(\left(1.8\right)\) | \(\left(1.8\right)\) |
| 8 | \(a+\frac{\sqrt{b+c}}{2}\) | \(a+\frac{\sqrt{b+c}}{2}\) | \(a+\frac{\sqrt{b+c}}{2}\) |
| 9 | \(\frac{\int\sqrt{1+{y^{'}(t)^{2}}}dt}{\int\sqrt{{x^{'}(t)^{2}}+{y^{'}(t)^{2}}}dt}\) | \(\frac{\int\sqrt{1+{y^{2}(t)^{2}}dt}dt}{\int\sqrt{{x^{2}}+{y^{2}}}}\) | \(\frac{\int\sqrt{1+{y^{2}(t)^{2}}dt}dt}{\int\sqrt{x^{2}}}\) |
| 10 | \({{T+\sin{a}^{M}}\leq4.45}\) | \({T+\sin{a^{M}}\leq4.45}\) | \({T+\sin{a^{M}}\leq4.45}\) |
| 11 | \(\frac{5}{x+1}+\frac{5}{{x^{2}}+x}\) | \(\frac{5}{x+1}+\frac{5}{{x^{2}}+x}\) | \(\frac{5}{x+1}+\frac{5}{{x^{2}}+x}\) |
| 12 | \(x_x^x+y_y^y+z_z^z-x-y-z\) | \(x_x^x+y_y^y+z_z^z-x-y-z\) | \(x_x^x+y_y^y+z_z^z-x-y-z\) |
| 13 | \(14\times87\neq-196\) | \(14\times87\neq-196\) | \(14\times87\neq-196\) |
| 14 | \(\mbox{d}\) | \(\mbox{d}\) | \(\mbox{d}\) |
| 15 | \(\sum_{i=1}^{n}i=\frac{1}{2}n(n+1)\) | \(\sum_{i=1}^{n}i=\frac{1}{2}n(n+1)\) | \(\sum_{i=1}^{n}i=\frac{1}{2}n(n+1)\) |
We note the following discrepancies:
- 0-th row: beam search surrounds the
owith ambox - 1-st row: beam search adds an extra
}at the end - 5-th row: both beam search and greedy decoding produce incorrect outputs towards the end where it gets cramped
- 9-th row: both beam search and greedy decoding produce incorrect outputs towards the end
In practice, we would normally use an evaluation metric such as edit distance or BLEU score rather than manual inspection.
References
-
Xie, Y., et al. (2023). ICDAR 2023 CROHME: Competition on Recognition of Handwritten Mathematical Expressions. ICDAR 2023. ↩
-
Moi, A., & Patry, N. (2023). HuggingFace’s Tokenizers. Computer software. ↩
-
Zhao, W. Q., Gao, L.C., Yan, Z. Y., Du, L. & Zhang, Z.Y. (2021). Handwritten Mathematical Expression Recognition with Bidirectionally Trained Transformer. ICDAR 2021. ↩
